授 课 计 划
2018 — 2019 学年第一学期
学 院： 数学科学学院
课程名称： 数学分析1
课程编码： 09A01030
课程类别： 专业基础课
计划学时： 80
学 分： 5.0
授课时间： 2018.9-2019.1
授课地点： 教 学 班：
授课教师：
填报日期： 2018年 9 月 10 日
数学分析是数学院各专业的必修专业基础课，分别在第一、二、三学期讲授数学分析1、数学分析2、数学分析3。数学分析1的基本内容包括：实数集与实数、数列极限、函数极限、函数的连续性、导数和微分、微分中值定理和不定式极限。本课程的教学目的是使学生获得数学分析基本概念、基本理论和基本方法，通过对极限理论和微分理论的解读和把握，提高学生的数学素养，使学生对近代数学的思想和方法得到深刻的理解和掌握，进而对后继课程学习和今后的工作打下坚实的基础。通过本课程的学习，学生应该熟练掌握各种概念的精确定义，深刻理解数学分析的基本理论，在数学的严密性和逻辑性方面得到严格的训练，进而灵活运用数学分析的基本方法，处理一些实际问题。本课程授课方式以课堂讲授为主，课下自学和练习为辅。
在学习本课程的过程中，学生要加强对基本概念和基本理论的学习，精读教材，按时独立完成作业，加强基本能力的培养和训练。要求学生学完本课程后，具有准确表述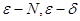
语言的能力，对概念的认识、理解和相互串联的能力，对数学问题的条件和结论的合理设计能力，对极限、微分的准确计算能力，进行简单的理论研究和应用研究的能力，对问题的独立思考能力。
推荐教材：华东师范大学数学系 编，《数学分析》（第四版）上册，高等教育出版社，2010年。
参考书目：（1）邓东皋、尹小玲编著《数学分析简明教程》上、下册，高等教育出版社，1999年。
（2）陈纪修、於崇华、金路编著《数学分析》上、下册，高等教育出版社，1999
（3）裴礼文 编，《数学分析中的典型问题与方法》，高等教育出版社，1993年。
授课内容：
第一章 实数集与函数(12学时）
授课内容：
§3函数概念；§4具有某些特性的函数；习题课
授课内容：
第二章 数列极限（16学时）
§1数列极限概念
授课内容：
§2收敛数列的性质
习题课
授课内容：
§3数列极限存在的条件
第三章 函数极限（18学时）
授课内容：
§2函数极限性质
授课内容：
§3函数极限存在的条件
§4两个重要极限
授课内容：
§5无穷大量与无穷小量
习题课
第四章 函数的连续性（16学时）
§1连续性概念
授课内容：
§1连续性概念
§2连续函数的性质
授课内容：
§2连续函数的性质
§3初等函数的连续性
授课内容：
第五章 导数和微分（18学时）
§2求导法则
授课内容：
§2求导法则
§3参变量函数的导数
授课内容：
§4高阶导数
§5微分
习题课
授课内容：习题课
